Power

A review of Erich Lehmann's last book, Fisher, Neyman, and the Creation of Classical Statistics.

---

Two months ago, a study came out in JAMA which compared the effectiveness of the antidepressant escitalopram to placebo for long-term major adverse cardiac events (MACE).

The authors explained in the methods section of their paper how they calculated their sample size and what differences they were looking for between groups.

First, they used some previously published data to get an idea for incidence rates,

“Because previous studies in this field have shown conflicting results, there was no appropriate reference for power calculation within the designated sample size. The KAMIR study reported a 10.9% incidence of major adverse cardiac events (MACE) over 1 year… Therefore, approximately 50% MACE incidence was expected during a 5-year follow-up.”

Then, they calculated their sample size based on some differences they were interested in finding,

“Assuming 2-sided tests, α = .05, and a follow-up sample size of 300, the expected power was 70% and 96% for detecting 10% and 15% group differences, respectively.”

So far so good.

Then, we get to the results,

---

---

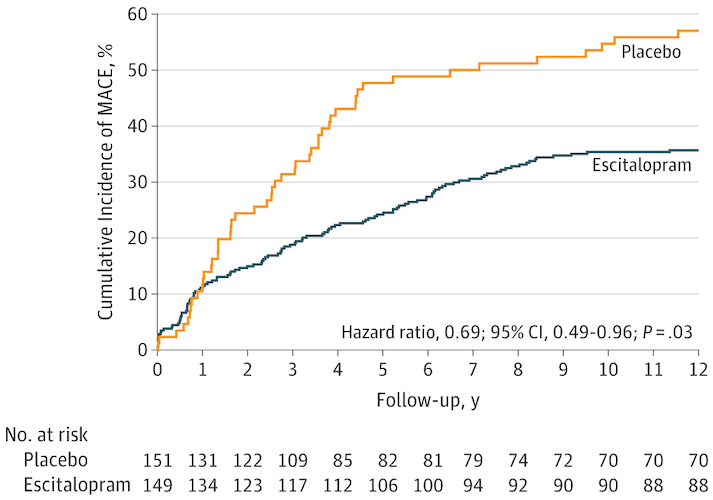
“A significant difference was found: composite MACE incidence was 40.9% (61/149) in the escitalopram group and 53.6% (81/151) in the placebo group (hazard ratio [HR], 0.69; 95% CI, 0.49-0.96; P = .03). The model assumption was met (Schoenfeld P = .48). The estimated statistical power to detect the observed difference in MACE incidence rates between the 2 groups was 89.7%.”

Ouch. This issue ended up bothering me so much that I wrote a letter to the editor (LTE) to point out the issue. Unfortunately, the LTE got rejected, but Andrew Althouse suggested that I discuss this over at DataMethods, so I did, and I also discussed it on Twitter but also wanted to publish the LTE on my blog. Here it is.

This letter has now been preprinted on arXiv.

In a similar tale, a group of surgeons published a methodological article advocating this practice of calculating observed power, which I further discuss here.

A discussion of events that transpired in the past year, where a group of surgical researchers promoted calculating post-hoc power using the observed effect size, despite warnings from several statisticians.